Recently, I needed to find a formula that predicted how often an event happens based on a percentage value. The challenge was to make sure the formula worked well for all reasonable inputs, without giving unrealistic results.
In his book “How to Measure Anything: Finding the Value of Intangibles in Business”, Douglas Hubbard explains how the act of measurement is not about getting an absolute value without any errors, but about reducing uncertainty about something we know little or nothing about.
He explains how, for example, the first measurements of the gravitational constant "g" weren’t very accurate, but still provided a good approximation that helped solve problems. As scientists gathered more data, they were able to refine their values.
This was exactly my goal: to find an equation that gave a first approximation of the “true” formula based on the information I had, one that I could use to make predictions and then refine as I gathered more data.
Problem Definition
These were my constraints, based on three events measured at different points in time (plus the added case for 0%)
∀x>0,f(x)>0
f(0) = 0
f(0.37) = 12.2
f(0.46) = 26
f(0.91) = 90Which looks like this:
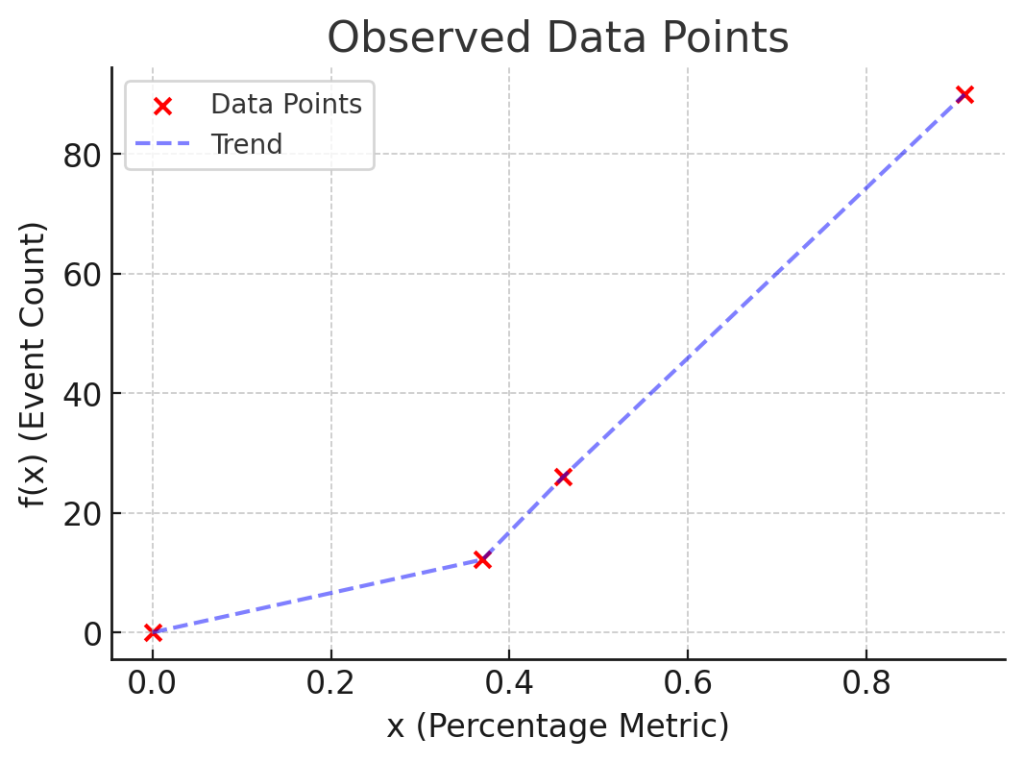
I needed one equation, but we can see from the chart that the data appears to have two or more distinct segments rather than following a single curve. There are many types of equations that we could potentially fit: quadratic, cubic, exponential, etc. I can easily discard linear and logarithmic just by looking at the chart.
With this information, I could use some tools to find the equation I was looking for.
Using AI
I asked ChatGPT to find this equation, and this was the result:
f(x) = 16.4 × x^3.2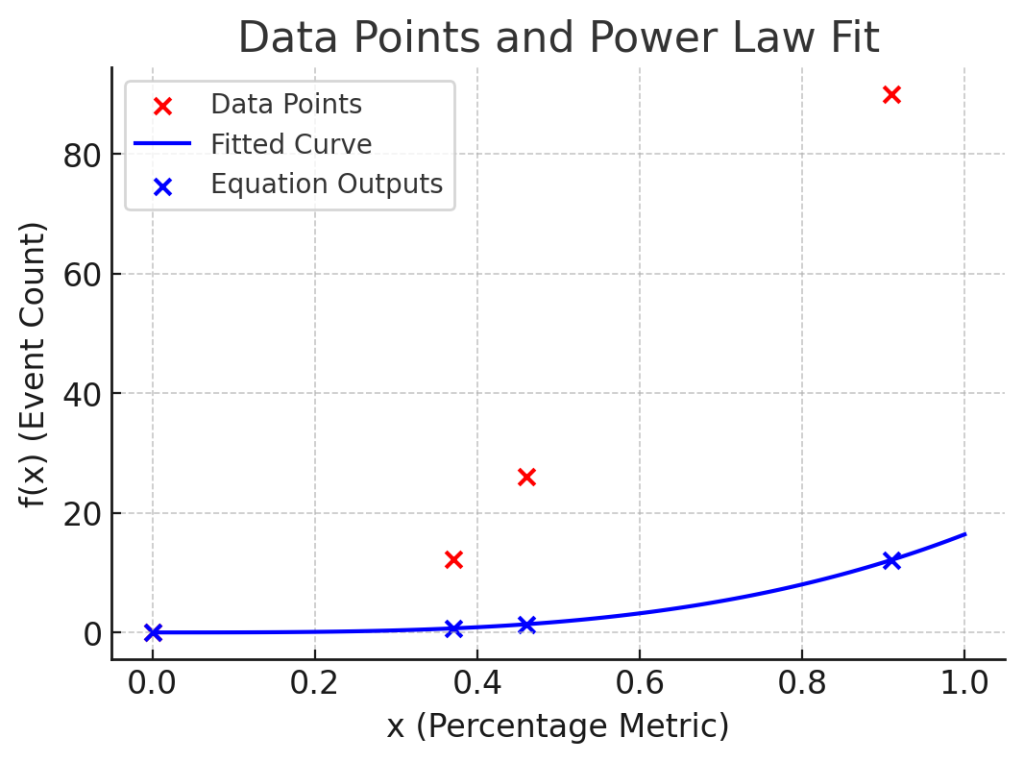
It is clear that the error of this equation is too large to consider this a viable solution, as it simply produced a single guess based on pattern recognition.
Since AI wasn’t giving me a reasonably good answer, I needed a different approach, one that could evolve towards a better solution instead of just spitting out a single guess, so I asked it to implement a Genetic Algorithm based on my constraints.
Using Genetic Algorithms
What are Genetic Algorithms?
As we know thanks to Charles Darwin and his Theory of Evolution, it’s usually the better suited individuals of a population that survive and have offspring. And we’ve also learnt that sometimes individuals have random mutations that make them slightly different from either of their parents.
Apparently, it was Alan Turing that first suggested using this approach in computers back in 1950, so this idea is not new, but still useful in some cases, like this.
The idea is to represent a population of individuals that, based on their attributes, are more fit than others to survive, that reproduce, and whose children may have mutations. Let’s see how this is implemented in practice.
Genetic Algorithms Implementation
First, we need to represent individuals. In my case, an individual was a type of equation (quadratic, cubic, etc), and the coefficients for that equation. These are the genes of my individuals.
Then, we need a fitness function that can tell us if this individual will reproduce or not. Only the better suited individuals will pass their genes to the next generations. In my case, the fitness function is implemented as the absolute value between the expected value minus the evaluated value for event data available, where a lower value is better. Whenever I got negative values, I added a penalty value that would make that individual less fit to survive.
The algorithm starts with a large population of randomly generated individuals. From there, it runs through several cycles, selecting the fittest, mixing their traits, and introducing small mutations along the way. In my case, I used a population of 10,000 and kept going until I found an equation with an error below 0.01, or until I hit 20,000 generations.
Selection: we evaluate every individual using the fitness function, and select the individuals that had the best score (lower value in my case).
Crossover: this is the part kids probably shouldn’t be watching. Two individuals mix their genes, and voilà! New equations are born. In my case, I picked two at random, kept the equation type of the first, and randomly chose coefficients from either parent.
Mutation: for every new individual, there is a chance that one or more of their attributes will change. In my implementation, every coefficient had a 5% chance to change to a random value.
Evaluating The Solution
After running my genetic algorithm, I found this equation:
f(x) = 3.104 × e^(3.700x)Which behaves like this:
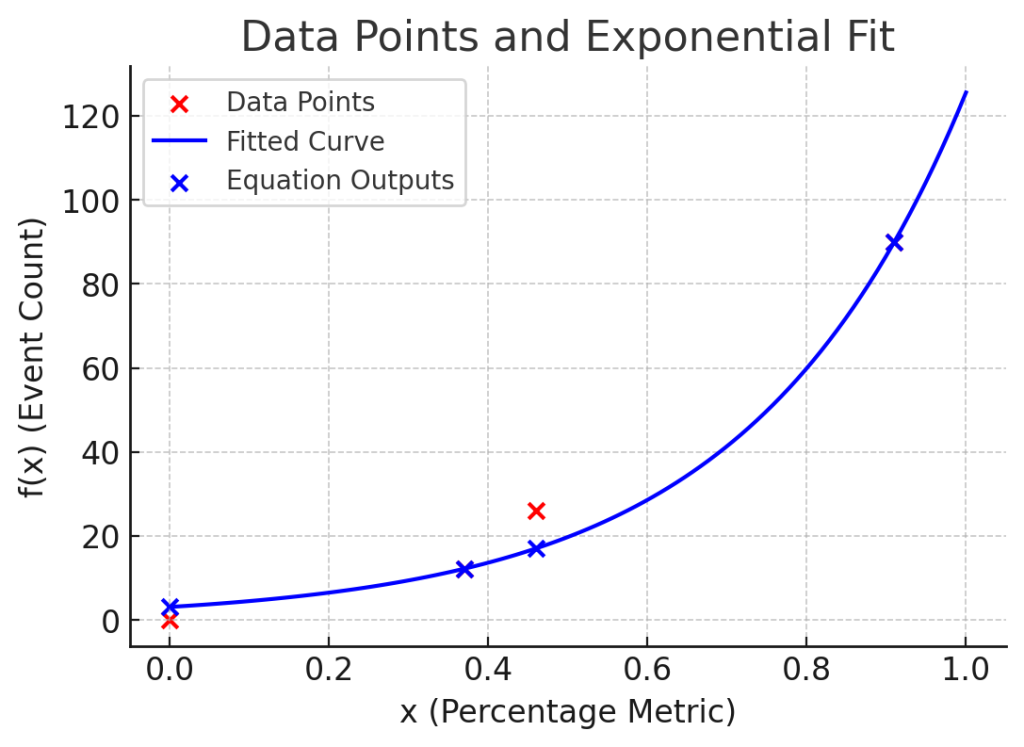
When validating a model like this, we’d usually need a training set and a test set. The training set (usually around 70% of the data) is used to generate the results, and the rest to validate how good it is.
In my case, this was not practical, because I only had four data points, and I’d have had to use three for training and one for testing.
Although this approach is not rigorous enough to be published in a paper, it still serves my purpose of reducing uncertainty about something I knew very little about, where obtaining more data points is too expensive to make it practical.
You can follow this link to see the code: https://github.com/jm-armijo/ga-equation-finder
Known Limitations
Genetic Algorithms are a great tool if used for the right problem. To be effective, we require a clear criteria to define the fitness, and that can execute efficiently, otherwise we won’t generate enough generations in a reasonable amount of time. In my case, the fitness function was very simple and was executed very quickly.
Another limitation is that these algorithms tend to find local optimum solutions. Given the constraints on what type of equations to evaluate, I could guarantee that I would not get trapped in a local maximum. Had I tried a sinusoidal equation, things could have been different.
Final thoughts
If this had been a personal project, I would’ve written the code myself because it’s fun. But this was a real problem with time pressure, so I used the tools that got me there faster.
I felt comfortable doing this because I already know how Genetic Algorithms work. However, if you haven’t written one yourself before, I really recommend giving it a go at least once. It’s not just about solving a problem; it’s a great way to learn the technique.
It was interesting to see that despite the rise of AI, there are still problems it can’t solve. This serves as another reminder that, while incredibly useful, these tools are not almighty, at least for now.
Cheers,
José Miguel
Share if you find this content useful, and Follow me on LinkedIn to be notified of new articles.